「一陸技 工学A 令和2年11月期第1回A19」の問題を解いてみました。
当サイトが把握している平成23年7月期以降の出題例はなく、おそらく新問題と思われます。
【追記】その後、令和5年01月期第2回でも出題されました。
なお、本記事の図や解説は必ずしも学術的に正しいとは限りません。
あくまで個人の見解であることをご承知おきください。
解説
問題はこちらとなります。
π型抵抗減衰器というものらしいです。

ここで、回路図に少し書き加えましょう。
問題文より、
・入力端にZ0の信号源
・出力単にZ0の負荷
が接続されると記載されているので、次のように書き加えます。
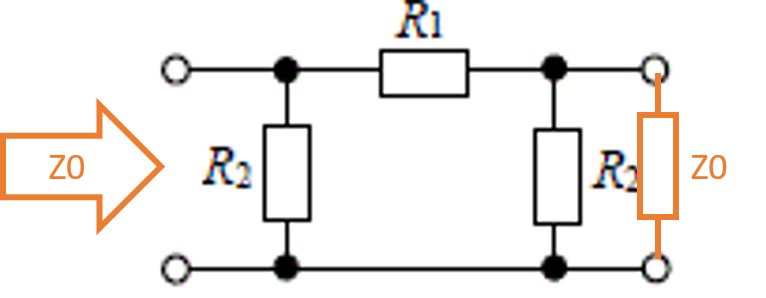
さらに解きやすいように回路を変形しましょう。
このように変形することで、回路の直列/並列の関係がわかりやすくなります。
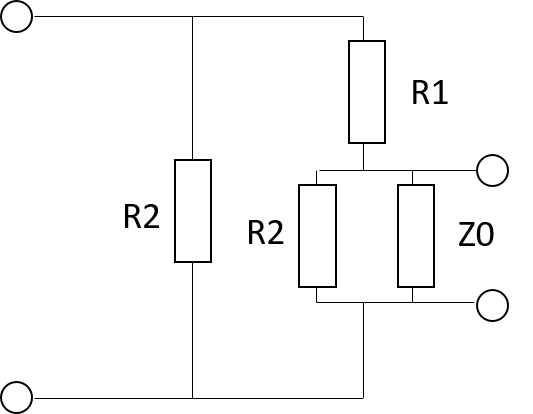
この回路のうち、並列の部分の合成抵抗をR3として求めてみましょう。
この部分ですよ。
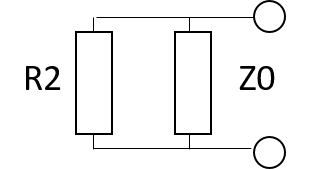
並列回路の合成抵抗の公式は、知らないとお話にならない重要公式です。
忘れていた方は思い出しましょう。
$$R_3=\frac{R_2Z_0}{R_2+Z_0}$$そうすると、このようにシンプルな回路図になりますね。
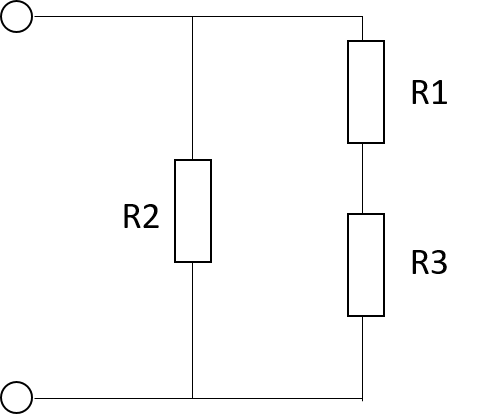
これより、
$$Z_0=\frac{R_2\times(R_1+R_3)}{R_2+(R_1+R_3)}$$ $$=\frac{R_2\times(R_1+\frac{R_2Z_0}{R_2+Z_0})}{R_2+(R_1+\frac{R_2Z_0}{R_2+Z_0})} ・・・・・(1)$$次に減衰量14[dB]の真数を求めましょう。
お待ちかねのログ計算です。
苦手意識持たれてる方もいるかもしれませんが、
ログ計算抜きに一陸技の合格は厳しいです。
頑張りましょう!
ログ計算は、頭に10が付くものと20が付くものとあって混乱しませんか?
電圧比なら20、電力比なら10です。
$$電圧比:20\log_{10} X$$ $$電力比:10\log_{10} X$$この問題の場合は問題文には明確に書いていませんが、電圧比のことらしいです。
というわけで、20の方を採用しましょう。
減衰量14[dB]の真数をnとします。
$$20\log_{10} n = -14$$よって、
$$\log_{10} n = -\frac{14}{20}$$ $$=-0.7$$ $$=-1+0.3$$ $$=\log_{10} 10^{-1} + \log_{10} 2$$ $$=\log_{10} \frac{2}{10}$$ $$=\log_{10} \frac{1}{5}$$よって、減衰量の真数は
$$n=\frac{1}{5}$$ということは、下の図のとおり電圧比は4:1となります。
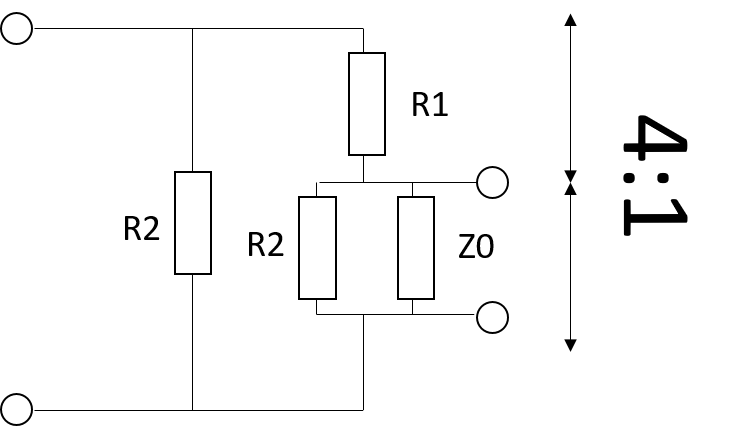
よって、R1を求める式は次のようになります。
ちなみになぜR1を求める式を作るかというと、(1)でR1をキャンセルしてR2を求めるためです。
$$R_1 = \frac{4R_2Z0}{R_2+Z_0}・・・・・(2)$$(2)を(1)に代入します。
すみません、LaTex入力が大変なので途中の計算は省きます。
頑張って計算するとこのようになります。
$$Z_0 = \frac{R_2\times(R_1+\frac{R_2Z_0}{R_2+Z_0})}{R_2+(R_1+\frac{R_2Z_0}{R_2+Z_0})}$$ $$=\frac{5R_2Z_0}{R_2+6Z_0}$$さらに整理すると、R2が求められます。
(計算過程は省きました)
類似問題から今後の問題を予想する
実はT型抵抗減衰器と呼ばれるものの出題例は多くあります。
このような問題です。


上の二つの問題をよーく見比べてみてください。
何が違いますか?
・令和2年11月期第2回A19はR1を求める問題
・ 平成30年07月期A19はR2を求める問題
です。
もしかしたら、π型抵抗減衰器の問題も次はR1を求める問題が出るかもしれません。
また、次のように減衰量が変えてあるパターンもあります。
上の問題では減衰量が14[dB]でしたが、次の問題は12[dB]です。

もしかしたら、π型抵抗減衰器の問題も次は減衰量の値を変えた問題が出るかもしれません。
これらのような少し変えてある問題にも対応できるようにしておきたいところです。
求める抵抗が変わる場合の解き方
次の問題を解いてみましょう。

(1)の式は共通で使えます。
$$Z_0=\frac{R_2\times(R_1+\frac{R_2Z_0}{R_2+Z_0})}{R_2+(R_1+\frac{R_2Z_0}{R_2+Z_0})} ・・・・・(1)$$(2)の式をR2を求める式に変形します。
$$R_1 = \frac{3R_2Z0}{R_2+Z_0}・・・・・(2)$$これを変形して、
$$R_2 = \frac{R_1Z0}{4Z_0-R_1}・・・・・(2)’$$(2)’を(1)に代入して、頑張って計算するとR1が得られます。
$$R_1=\frac{12}{5}Z_0$$減衰量の値が変わる場合の解き方
次の問題を解いてみましょう。

(1)の式は共通で使えます。
$$Z_0=\frac{R_2\times(R_1+\frac{R_2Z_0}{R_2+Z_0})}{R_2+(R_1+\frac{R_2Z_0}{R_2+Z_0})} ・・・・・(1)$$減衰量12[dB]の真数をnとします。
$$20\log_{10} n = -12$$よって、
$$\log_{10} n = -\frac{12}{20}$$ $$=-0.6$$ $$=-2×0.3$$ $$=-2\log_{10} 2$$ $$=\log_{10} 2^{-2}$$ $$=\log_{10} \frac{1}{4}$$よって、減衰量の真数は
$$n=\frac{1}{4}$$これより、電圧比は3:1なので
$$R_1 : \frac{R_2Z_0}{R_2+Z_0} = 3 : 1 $$整理するとR1を求める式は次のようになります。
$$R_1 = \frac{3R_2Z_0}{R_2+Z_0}・・・・・(2)”$$(2)”を(1)に代入します。
頑張って計算するとこのようになります。
$$Z_0 = \frac{R_2\times(R_1+\frac{R_2Z_0}{R_2+Z_0})}{R_2+(R_1+\frac{R_2Z_0}{R_2+Z_0})}$$ $$=\frac{4R_2Z_0}{R_2+5Z_0}$$さらに整理すると、R2が求められます。
(計算過程は省きました)
T型抵抗減衰器の問題には減衰量が6[dB]と20[dB]の出題例もあります。
同じように計算できるので、できればやってみてください。
【続報】令和5年01月期第2回で出題されました
減衰量の値が変わった場合の問題が令和5年01月期第2回で出題されました。

ただし、減衰量は予想したものにはなかった8dBでした。
ひっかけ問題にも対応できるようにしよう
この記事で取り上げた問題だけではなく全般的に言えることですが、
問題を解く際は「値などが変わるとしたらどこか」「変わっても対応できるか」を考えながら解くようにしましょう。
値だけでなく、空欄の箇所やもっと細かいところが変わる場合もあります。
最近の傾向を見ていると、一見気が付かないようなより細かい箇所が変更されていることが多いように感じるのでよく注意してください。
そのような例を次の記事で紹介してありますので、参考に見てみてください。
また、当サイトの同じパターンの問題を見る機能を使うと、変わりやすいポイントのカンがある程度鍛えられると思いますので、ぜひご活用ください。