この方程式が何かわかりますか?
$$ R_{max} = \sqrt[4]{\frac{PG^2λ^2σ}{(4π)^3S_{min}}}$$
一陸技の無線工学Aで出てくるレーダー方程式です。
とても複雑な方程式ですよね。
管理人が受験したときはなかなか覚えられなくて、試験直前まで公式をガン見して試験始まった途端に問題用紙に書き写した思い出があります(笑)
みなさまはどうやって覚えたのか、Twitterで聞いてみました。
レーダー方程式の覚え方は3種類
覚え方は大きくわけて次の3種類でした。
- 丸暗記ではなく導出した
- 直前に無理やり覚えて問題用紙に書き写した
- 語呂合わせで覚えた
一番多かったのは、丸暗記ではなく導出して覚えたというコメントでした。
Twitterで頂いた声を紹介します。
丸暗記ではなく導出した
直前に無理やり覚えて問題用紙に書き写した
語呂合わせで覚えた
4乗根とは?
4乗根てそもそもなんだっけ?という声もありました。
4乗根とは、4回かけるとその数になる数です。
たとえば、
$$ 3 = \sqrt[4]{3} \times \sqrt[4]{3} \times \sqrt[4]{3} \times \sqrt[4]{3}$$
です。
2乗根と比べてあまり見慣れないですよね。
久しぶりに数学に触れる社会人は特に「なんだっけ?」となってしまう気持ちわかります。
レーダー方程式とは?
そもそもレーダー方程式とはなんでしょうか。
一般にレーダー方程式というのは次の数式のことだそうです。
$$ S = \frac{PG^2λ^2σ}{(4π)^3R^4}$$
S:受信電力
P:レーダーアンテナから発射される電波の電力
G:アンテナの利得
λ:電波の波長
σ:有効反射断面積
R:距離
この数式によって、レーダーを目標に向けて発射した際に目標物からの跳ね返りによって受信される電力を求めることができます。
ここで、行きと帰りの経路があることをイメージしておいてください。あとで使います。
①行き:送信→目標物
②帰り:受信←目標物
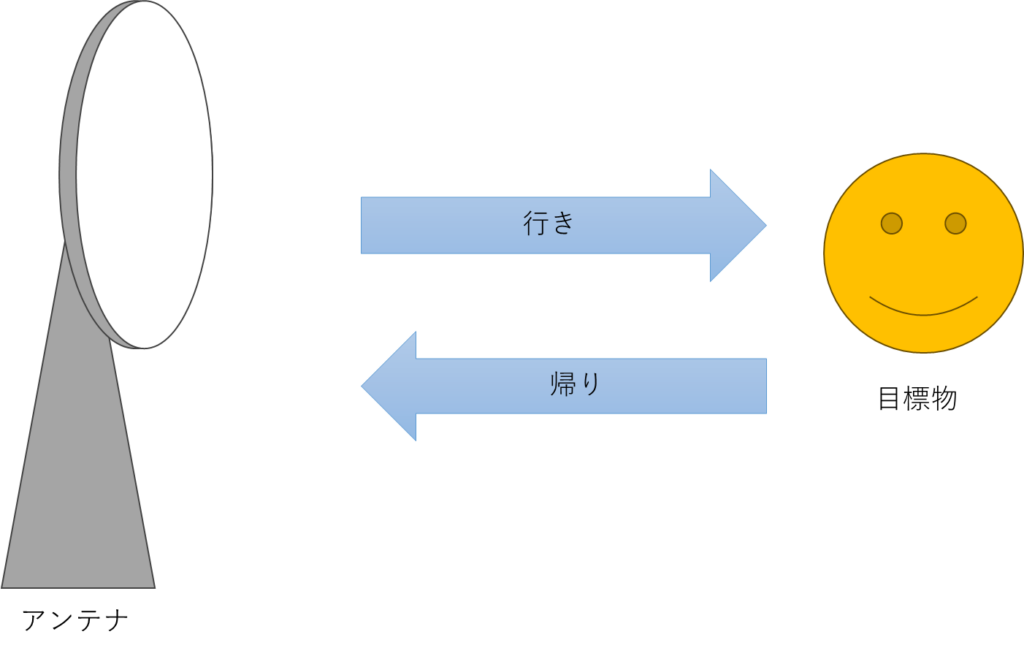
ここまでの数式の導出の過程はできれば理解しておいた方が良いです。
ですが、丸暗記で乗り切った管理人が説明するより、詳しく説明されているサイトにお任せした方が良さそうなので、参考になりそうなサイトを紹介します。
レーダー方程式・・・範囲は無線工学Aだが無線工学Bの知識も必要
(「さて、雨の日は勉強でもするか。」)
レーダー方程式
(「物理学のフィロソフィア」)
管理人の愛用している参考書にもレーダー方程式の導出が書いてありました。
受験当時は丸暗記で済ませてしまいましたが、改めて読み直すとよく理解ができました。
これより、受信電力Sは距離Rが遠いほど小さくなることがわかります。
そしてその限界値を表したものが次の数式です。
$$ S_{min} = \frac{PG^2λ^2σ}{(4π)^3R_{max}^4}$$
Smin:最小受信電力
Rmax:最大探知距離
冒頭で紹介したRmaxを求める式は、上記の式を変形したものです。
$$ R_{max} = \sqrt[4]{\frac{PG^2λ^2σ}{(4π)^3S_{min}}}$$
レーダー方程式の覚え方のイメージ
レーダー方程式の導出の過程を知っていると、覚え方のイメージが付きやすくなります。
きちんとした詳しい説明は別サイト、参考書に任せるとして、ここでは導出の過程を踏まえてムセンボーヤ!!的ざっくり覚え方のイメージを紹介したいと思います。
Sminを求める式で覚え方をイメージしていきましょう。
$$ S_{min} = \frac{PG^2λ^2σ}{(4π)^3R_{max}^4}$$
なぜRmaxが4乗なのか?
分母に注目してみてください。
$$ (4π)^3R_{max}^4$$
何か、ピンと来ませんか?
そう、なんか球っぽいですよね?
なんたって、πとかRとかありますからね!(バカみたいですみません)
レーダーから発射された電力は、球面上に広がります。(無指向性アンテナの場合)
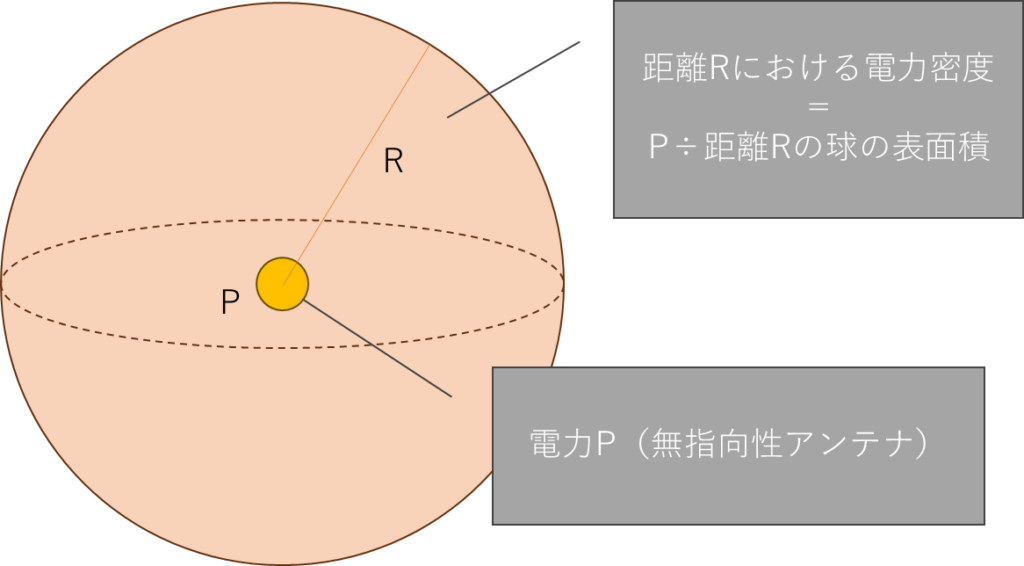
距離Rにおける電力密度は、元々の電力を距離Rの球の表面積で割ったものとなります。
$$ 球の表面積=4πR^2$$
$$ 距離Rにおける電力密度=\frac{P}{4πR^2}$$
さきほど、行きと帰りの経路があることをイメージしてくださいとお伝えしましたね。
行きと帰りの往復分、球の表面積が掛け合わされています。

球の表面積のRは2乗ですから、往復分で4乗となります。
なぜ4πは3乗なのか
Rと同様分母に注目します。なんか球っぽい観点は同じです。
$$ (4π)^3R_{max}^4$$
球の表面積が往復分かかるなら、4πは2乗では?と思いますよね。
なぜ2乗ではなくて3乗なのでしょうか。
実はアンテナの有効受信断面積とアンテナ利得Gには次の公式があります。
$$A_{r}=\frac{Gλ^2}{4π}$$
Ar:アンテナの有効受信断面積
詳しくは説明しませんが、この公式がレーダー方程式の導出の過程で掛け合わされています。
この公式はレーダー方程式と合わせて必ず覚えておいてください。
問題文中で与えられる場合もありますが、与えられない場合もあります。
公式の中に4πが含まれていますね。
4πは次の3回掛け合わされているため3乗となります。
①行き:送信→目標物
②帰り:受信←目標物
③有効受信断面積の公式
なぜGが2乗なのか
実際にはレーダーは無指向性ではなく、指向性を持って発射されます。
そのため、無指向性のアンテナよりも電力密度が大きくなります。
それを数式上で表しているのがアンテナの利得Gです。
でも、それだけだとGは1乗です。
さきほど、次の公式がレーダー方程式の導出の過程で掛け合わされているとお伝えしました。
Gが含まれますね。
$$A_{r}=\frac{Gλ^2}{4π}$$
Gは次の2回掛け合わされているため2乗になります。
①アンテナの指向性
②有効受信断面積の公式
レーダー方程式を使う問題に挑戦してみよう
一陸技工学A令和4年01月期第1回A12

レーダー方程式よりそれぞれの関係性を考えましょう。
計算していくと4乗根が2乗根に変形できます。
問題が解けたらリンク先の「同じパターンの問題を見る」でほかの問題も見てみましょう。
次の問題では(3)で倍にする対象が違います。
でも解き方がわかっていれば対応できますね。

一陸技工学A令和5年07月期第2回A12
こちらの問題はさらに難易度が高いです。

ただレーダー方程式に当てはめていけば解ける問題ではありません。
非常に計算力が試される問題です。
解くためのポイントは以下です。
- dBではなく真数で計算する(log計算に慣れましょう)
- 単位を合わせて計算する(mWやkmなどに注意!)
- アンテナの実効面積の公式を活用して与えられていないGを導出する
問題が解けたらリンク先の「同じパターンの問題を見る」でほかの問題も見てみましょう。

こちらの問題はアンテナの実効面積の公式が与えられていません。
でも、使います。ですから、覚えておいてください。
$$A_{r}=\frac{Gλ^2}{4π}$$
まとめ
レーダー方程式の覚え方は、丸暗記ではなく導出して覚えたという声が一番多かったです。
管理人が受験したときは丸暗記で済ませてしまいましたが、実際に導出の過程を勉強すると公式の覚え方のイメージが格段に付きやすくなったことを実感しました。
導出の詳細な過程は別のサイトや参考書に任せて、この記事では導出の過程を踏まえた覚え方のイメージを紹介させていただきました。
無線工学Aは新問題が多く出題されるので、今後レーダー方程式の新問題が出題されてもおかしくありません。
ですが、導出まで理解してしまえば、新問題が出題されてもこわくありませんね。
受験当時の管理人のように面倒くさがらずに、導出の過程を理解していただくのがおすすめです。